Фурье Трансформация - Компьютерная Графика

Ряд Фурье

Jean Baptiste Joseph Baron de Fourier (1768-1830) в "Аналитической Теории Тепла" (Paris 1822) вывел следующий закон:

Любая периодическая функция f(x) может быть представлена в виде суммы констант и рядов волн косинусов и синусов - так называемый Ряд Фурье:

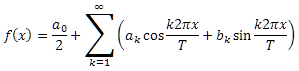
Обратите внимание, что индекс суммирования k встречается в виде множителя частоты в обоих аргументах.
Произвольные периодические функции могут быть выражены в виде такого ряда.

Упрощенный Ряд Фурье состоит из:

Константы a₀/2, где a₀ - это среднее значение функции f(x).
Если периодическая функция имеет период T, то мы должны добавить функции косинуса и синуса с периодом
T (1/T = базовая частота) с амплитудами (которые еще надо вычислить) a₁ для косинуса и b₁ для синуса: f(x) = a₀/2 +a₁*cos(x) + b₁*sin(x).
Затем следуют косинус и синус с полупериодом =T/2 и амплитудами (которые нужно вычислить) a₂ и b₂:
f(x) = a₀/2 +a₁*cos(x) + b₁*sin(x) + a₂*cos(2*x) + b₂*sin(2*x).
Снова другие два элемента с периодом =T/3 и амплитудами (которые нужно вычислить) a₃ и b₃ и так далее с парами косинусов и синусов с периодом T , деленным на целые числа T/4, T/5 ...
Знаменатель T , как и множитель k возникают из-за того, что деление T на k эквивалентно умножению на частоту: x*2*Pi/(T/k) = k*x*2*Pi/T.

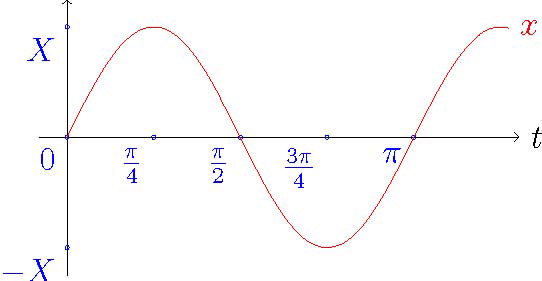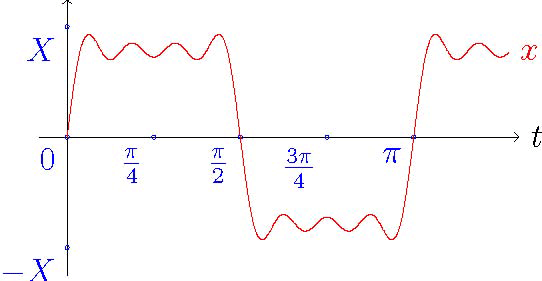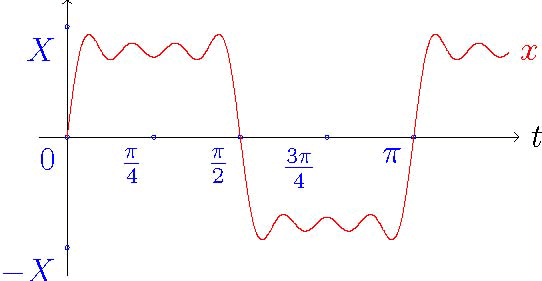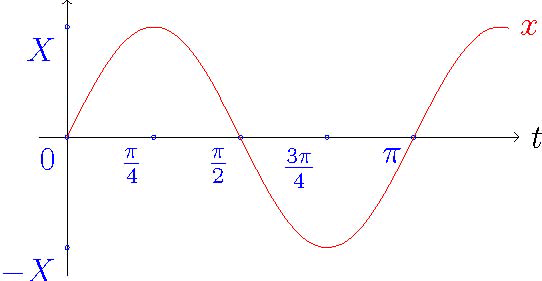
Резонаторы

Фурье, как физик, был вдохновлен физическими явлениями:
очень просто произвести неприятные диссонансные звуки с помощью струнных инструментов, даже если струны просто вибрируют в своих гармониках: произвольная смесь чистых частот обычно производят диссонансы и очень редкие звучат красиво. Этот интуитивный вывод оказался поворотным для научного понимания устройства волн.

Пример 1: В улитке внутреннего уха существует жидкостно-механическая система с гармоническими точками, несущими сенсорные клетки. Эти волосковые клетки замеряют перемещения резонаторной мембраны. Электрический поверхностный потенциал волосковых клеток изменяется в зависимости от их изгиба, возникающего от звуковых волн. Это аналогично изменению напряжения тока, идущего от микрофона в соответствии с движением микрофонной мембраны. Волосковые клетки высвобождают нейротрансмиттеры во внеклеточное пространство, которые вызывают нервные импульсы определенного волокна вторичного нейрона, несущего информацию об амплитуде специфической характерной частоты.

Пример 2: Электрическая схема катушки и параллельного конденсатора имеет определенную резонансную частоту. Такой резонатор определяет наличие или отсутствие одной определенной частоты в любом наборе частот внешнего сигнала и получает энергию возбуждения, когда соответствующая частота присутствует во внешнем сигнале. Там нет активного процесса, это просто эффект резонансного отклика.
Эти резонансные контуры являются основой электротехники звука.Упорядоченное множество резонансных контуров облучается произвольным сигналом, но только частоты, совместимые с резонатором, остаются на выходе. Эти выходные сигналы из разных резонаторов усиливаются и вновь перемешиваются и в результате получаются усиленный сигнал идентичный входящему, который только состоит из нескольких чистых частот, выходящих из резонаторов. Удивительно то, что сравнительно малый набор резонаторов достаточен для того, чтобы усилить произвольные волны.

Пример 3: Качели качаются с определенной частотой. Если вы хотите раскачать ребенка сильнее, то вы должны прикладывать усилия с определенной резонансной частотой. Невозможно усилить амплитуду качения, толкая постоянно или с другой частотой.

Резюме: преобразованием Фурье называется расщепление периодического колебания в вид конечной или бесконечной суммы гармонических колебаний кратных основной частоте, и его обратного суммирования, что означает, реконструкцию произвольной формы за счет сложения гармонических колебаний.

В синусы и косинусы рядов Фурье можно рассматривать как математические резонаторы по аналогии с электрическими резонаторами с возможностью обнаруживать присутствие определенных частот в смеси и при обнаружении таковых - получать количественную оценку их индивидуального вклада в общий смешанный сигнал = их относительных амплитуд (относительно половине средней амплитуды всей смеси).

Для простоты мы растягиваем период T до длины 2*Pi.
Жозе Фурье предложил гениальную идею:
(1) Он умножил оригинальный сигнал f(x) на чистые резонаторы cos(k*x) и sin(k*x). Для всех значений k он получил два результирующих сигнала f(x)*cos(k*x) и f(x)*sin((k*x) со следующими свойствами:
результаты всегда имеют положительный и отрицательные значения, даже в случае если оригинальная функция f(x) была только положительной или только отрицательной. Результат высоко положителен в месте, где гора встречается с горой или где долина встречается с долиной (= 1-й вариант) и глубоко отрицателен в месте, где гора встречает долину (=2-й вариант).
Когда вариант 1 встречается также часто, как вариант 2 в f(x)*cos(k*x) или f(x)*sin(k*x), то сумма равна 0 и f(x) не имеет ничего общего с cos(k*x) или sin(k*x).
Когда вариант 1 встречается чаще, чем вариант 2 в f(x)*cos(k*x) или f(x)*sin(k*x), то сумма положительна и f(x) и cos(k*x) или sin(k*x) имеют общую частоту k.
Если вариант 2 появляется чаще, чем вариант 1 в f(x)*cos(k*x) или f(x)*sin(k*x), то сумма отрицательна и f(x) и cos(k*x) или sin(k*x) имеют общую частоту k.

(2) подразумевая эти варианты, Фурье использовал суммы результирующих функций, как резонаторы. Суммы считаются, как интегралы от f(x)*cos(k*x)*dx и f(x)*sin(k*x)*dx в границах периода T.
Деление интегралов на T дает нормализованные резонансные отклики, так называемые Фурье коэффициенты: два отклика a_k и b_k для каждого резонансного теста с частотой k:

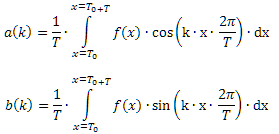
Пример

f(x) состоит из 3-х синусный кривых и шума

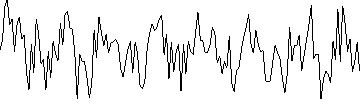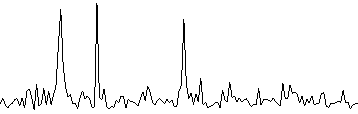
a_k²+b_k² (0 <= k < N)

Почему Cos и Sin?

Почему Фурье использовал два резонатора (cosine и sine) для теста частот? Почему cos или sin не работают в одиночку?
Ответ: Когда пик горы функции f(x) встречает нулевую отметку функции cos(k*x), результат имеет положительную и отрицательную половины, которые в сумме дают 0 даже если гора имеет тот же размер и форму, что и cos(k*x).
Для этого случая Фурье понадобился резонатор-близнец той же частоты, но сдвинутый на 90 градусов по фазе, чтобы быть уверенным, что хотя бы один из близнецов вступит в резонанс.
Электрические и другие физические резонаторы не требуют таких близнецов, так как без возбуждения они находятся в пассивном состоянии, не имея собственных колебаний. При возбуждении они переходят медленно в резонанс в той фазе, что и получаемый ими сигнал.

В отличие от математических, резонаторы Фурье всегда колеблются самостоятельно, без чувствительности к внешнему миру и без возможности синхронизации с ним. Они имеют характер постоянных испытательных волн, образующихся результирующими интегралами с возможными реальными f(x) волнами, и вам нужны две из них для любой гармонической частоты, чтобы быть уверенным, что, по крайней мере, одна из них придет в резонанс, с тем, что есть в f(x).

Позже мы увидим, что, когда вы принудительно фиксируете f(x) в фазе симметричной x=0, на самом деле одного резонатора Фурье будет достаточно (Косинусного Преобразования).

Резюме: Фурье строит два резонатора для испытания любой целочисленной частоты, начиная с базовой частоты 2*Pi/T. Испытание (Тест) - это умножение резонатора и сигнала и интегрирование этих результатов. Если положительные и отрицательные области компенсируются в 0, то Тест считается отрицательным, в противном случае считается положительным. Эта процедура далеко не элегантна или эффективна,- она является стратегией грубой силы. Она нуждается в чрезмерных вычислительных затратах, безнадежной вещью в докомпьютерную эпоху, когда никто не был в состоянии продемонстрировать данное преобразование.

Физические и Математические определения

В традициях 19-го века мы говорим в терминах Физики, так как это намного проще и интуитивнее, чем абстрактные и обобщенные математические определения.

Аналогия гармонической композиции = гармонический синтез:
Физика: суперпозиция = произвольную волновую форму можно составить из чистых волн.
Математика: сумма = любую периодическую функцию можно аппроксимировать суммами функций косинусов и синусов .

Аналогия целочисленности:
Физика: Любое колебание может быть построено из простых кратных ему по частоте волн = гармонических волн.
Пример: Струна, зажатая между двумя точками может колебаться только с частотой, кратной ее основной частоте, т.к. никакое движение невозможно в точках крепления. Невозможно создать колебание не кратное основной частоте (например 2,2 или 7,5) потому что такие колебания вырвут струну из точки крепления.
Математика: Любая произвольная периодическая функция f(x) является точкой в ортогональном векторном нормализованном пространстве, с базисными векторами cos(k) и sin(k).

Аналогия гармонической декомпозиции = гармонического анализа:
Физика: Каждое колебание может быть разделено с помощью резонаторов на компоненты. Количество резонаторов должно соответствовать количеству выделяемых чистых волн. Резонаторы должны быть настроены на частоты, кратные основной.
Математика: Фурье трансформация - это свертка функций f[x] с cosinus(k*arg) и sinus(k*arg) для всех кратных значений аргумента arg дополненных ортогональными координатами a_k и b_k.

Другие аналогии:

Физика

Математика

Время t

независимая переменная x

растяжение(t), звуковое давление(t), сила поля(t)

функция y = f(x)

базовая длина волны T

множитель L = 2*Pi/T

гармоника с длиной волны T/2, T/3, T/4 и т.д.

делители аргументов 2, 3, 4 и т.д.

резонатор k_той гармоники

базисные вектора cos(k*L) и sin(k*L)

a_k и b_k - резонансные отклики обоих k_тых резонаторов

a_k и b_k = результаты всертки

Дискретная Фурье Трансформация = DFT

Функции хранятся в компьютерах, главным образом, как дискретные, равноудаленные данные в виде одномерных массивов.
Независимо от этого, такие данные имеют периодичность и преобразование Фурье оказывается очень полезным для удаления нежелательных артефактов и снижения избыточности = сжатия. Жозеф Фурье никогда не думал о таких вещах, но сегодня они являются наиболее популярными приложениями его гармонического анализа.

Расчет значений a_k и b_k из дискретного потока данных следует правилам Фурье:
Дан сигнал f(x) в форме массива длиной N
N представляет период T и каждый резонатор представляется в виде массива длиной N.
Суммы от 0 до N-1 заменяют интегралы от T₀ до T₀+T.

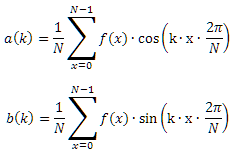
Так как нам нужно N cosine- и N синус-резонаторов, мы готовим резонаторы подходящим образом в виде квадратной
N*N-косинус-матрицы и синус-матрицы того же размера.
Умножение и суммирование теперь имеют форму скалярного умножения F (X) со всеми рядами обеих матриц.
Значения a_k и b_k вычисляются как N + N скалярное произведение: f(x) перемножается с одной строкой одной матрицы и делится на N. Количество необходимых операций с плавающей запятой огромен:
N*N расчеты косинусов плюс
N*N расчеты синусов плюс
2*N*N умножений плюс
2*N*N сложений плюс
2*N делений.

Пример Фурье декомпозиции сигнала с N=4

//C# program for this N=4 example
using System;
using System.Drawing;
using System.Windows.Forms;
using System.Text;

public class Form1 : Form
{ [STAThread] static void Main() { Application.Run( new Form1() ); }
  const int N = 4;
  float[] f0 = { 1f, 0f, 2f, 1f }, f1  = new float[N];
  float[,] cos = new float[N,N]  , sin = new float[N,N];
  float[]  a   = new float[N]    , b   = new float[N];
  StringBuilder sb = new StringBuilder();
  public Form1()
  { Text = "Fourier sample with N=4";
    Width = 320; Height = 400;
    int x, k;
    for ( k=0; k < N; k++ ) //prepare resonators
      for ( x=0; x < N; x++ )
      { cos[k,x] = Convert.ToSingle( Math.Cos( k*x*Math.PI/2.0 ) ) ;
        sin[k,x] = Convert.ToSingle( Math.Sin( k*x*Math.PI/2.0 ) ) ;
      }
    for ( k=0; k < N; k++ ) //Fourier transform
    { for ( x=0; x < N; x++ )
      { a[k] += f0[x] * cos[k,x]; //convolution
        b[k] += f0[x] * sin[k,x]; //convolution
      }
      a[k] /= N; b[k] /= N; //normalization
    }
    for ( k=0; k < N; k++ ) //back transform
      for ( x=0; x < N; x++ ) { f1[x] += a[k]*cos[k,x] + b[k]*sin[k,x]; }
    //compose output string
    sb.Append ("f0:\r\n");
    for ( x=0; x < N; x++ )   sb.Append( String.Format( "{0,5:F0}", f0[x]) );
    sb.Append( "\r\ncos:\r\n" );
    for ( k=0; k < N; k++ )
    { for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,5:F0}", cos[k,x]) );
      sb.Append( "\r\n" );
    }
    sb.Append( "sin:\r\n" );
    for ( k=0; k < N; k++ )
    { for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,5:F0}", sin[k,x]) );
      sb.Append( "\r\n" );
    }
    sb.Append( "a:\r\n" );
    for ( k=0; k < N; k++ )   sb.Append( String.Format( "{0,9:F2}", a[k] ) + "\r\n" );
    sb.Append( "b:\r\n" );
    for ( k=0; k < N; k++ )   sb.Append( String.Format( "{0,9:F2}", b[k] ) + "\r\n" );
    sb.Append( "f1:\r\n" );
    for ( x=0; x < N; x++ )   sb.Append( String.Format( "{0,5:F0}", f1[x]) );
    sb.Append( "\r\n" );
  }
  protected override void OnPaint( PaintEventArgs e )
  {  e.Graphics.DrawString( sb.ToString(), Font, new SolidBrush( Color.Red ), 0, 0 ); }
}

Оптимизированный алгоритм DFT

Следующая C#-программа
1) заполняет массив f0 с 3-мя частотами,
2) рассчитывает a_k и the b_k,
3) трансформирует обратно в массив f1,
4) формирует отчетную строку и выводит ее на экран,
5) при этом уменьшается расход памяти на 50% и расчетное время на 30% в сравнении с чистой формулой Фурье.

Программа получает выгоду от симметрии Фурье и уменьшает (без потери точности) количество a_k и b_kдо N/2+1. Причина: Оригинал f[x] имеет N элементов и, когда оба a_k и b_k имеют N элементов, создается редундантность 50%. Действительно, вторая часть массива значений a_k и b_k является зеркальным отражением первой:
1) когда N четное: a₀,...,a_N/2, a_N/2-1, a_N/2-2,...,a₁. Sample N=8: a,b,c,d,e,d,c,b
2) when N нечетное : a₀,...,a_N/2, a_N/2, a_N/2-1, a_N/2-2,...,a₁. Sample N=9: a,b,c,d,e,e,d,c,b

Вывод: нет необходимости рассчитывать более чем N/2+1 a_k и b_k. Это значит, что cos[,] и sin[,] резонаторы не должны быть квадратными матрицами - N/2+1 строк (с N колонками каждая) будет достаточно.

Существует еще одна интересная симметрия внутри оставшихся резонаторных матриц: верхняя правая половина идентична левой нижней половине с диагональной симметрией, потому что cos(k*x*arcus) идентичен cos(x*k*arcus) и тоже самое с sin(...). Поэтому можно вычислить верхний правый угол и отразить значения вниз влево.

Дальнейшая оптимизация:
1) Мы заполняем первый ряд и первую колонку cos(k*x*arcus) всегда в 1f , а sin(k*x*arcus) всегда в 0f без расчетов.
2) Мы устанавливаем a₀ всегда в среднее от f[x] , а b₀ всегда в 0f без расчетов.

Недостатки такой оптимизации:
1) код более сложен.
2) нормализация становится хитрой в сравнении с формулой Фурье: у нас дублируются все a_k и b_k кроме a₀,b₀ и a_N/2,b_N/2.

Вывод: Оптимизированное преобразование Фурье может быть удивительно быстрым.
В случаях с N <1000 нет необходимости использовать быстрое преобразование Фурье (FFT) с его ограничениями и неточностями.

using System;
using System.Drawing;
using System.Windows.Forms;
using System.Text;

public class Form1 : Form
{ [STAThread] static void Main() { Application.Run( new Form1() ); }
  const int N = 16;
  float[]  f0  = new float[N]      , f1  = new float[N];      //input, output
  float[,] cos = new float[N/2+1,N], sin = new float[N/2+1,N];//resonators
  float[]  a   = new float[N/2+1]  , b   = new float[N/2+1];  //Fourier coefficients
  StringBuilder sb = new StringBuilder();                     //one string takes all
  public Form1()
  { Text = "Fourier sample with N=16";
    Width = 500; Height = 600;
    int x, k;
    double arcus = 2*Math.PI/N, k_arcus, x_k_arcus;
    for ( x=0; x < N; x++ ) //input = mixture of 3 frequencies, just for fun
    { f0[x]  = (float)Math.Cos(     x * arcus );
      f0[x] += (float)Math.Sin( 3 * x * arcus );
      f0[x] += (float)Math.Cos( 6 * x * arcus + Math.PI/4 );
    }
    //prepare resonators
    for ( x=0; x <   N;  x++ ) { cos[0,x] = 1f; sin[0,x] = 0f; } //row no. 0
    for ( k=0; k <= N/2; k++ ) { cos[k,0] = 1f; sin[k,0] = 0f; } //column no. 0
    for ( k=1; k <= N/2; k++ ) //resonator rows 1 to N/2
    { k_arcus = k * arcus;
      for ( x=k; x < N; x++ )  //upper right triangle of cos[,] and sin[,]
      { x_k_arcus = x * k_arcus;
        cos[k,x] = Convert.ToSingle( Math.Cos( x_k_arcus ) ) ;
        sin[k,x] = Convert.ToSingle( Math.Sin( x_k_arcus ) ) ;
        if ( x <= N/2 && k != x )  //mirror to lower left except diagonal
        { cos[x,k] = cos[k,x]; sin[x,k] = sin[k,x]; }
      }
    }
    for ( x=0; x < N; x ++ ) a[0] += f0[x]; a[0] /= N; b[0] = 0f;
    for ( k=1; k <= N/2; k++ ) //Fourier transform
    { for ( x=0; x < N; x++ )
      { a[k] += f0[x] * cos[k,x]; //convolution
        b[k] += f0[x] * sin[k,x]; //convolution
      }
      if ( k < N/2 ) { a[k] *= 2f/N; b[k] *= 2f/N; } //doubling and normalization
      else           { a[k] /= N;    b[k] /= N;    } //normalization
    }
    for ( k=0; k <= N/2; k++ ) //back transform
      for ( x=0; x < N; x++ ) { f1[x] += a[k]*cos[k,x] + b[k]*sin[k,x]; }
    //compose output string
    sb.Append ("f0:\r\n");
    for ( x=0; x < N; x++ )   sb.Append( String.Format( "{0,6:F1}", f0[x]) );
    sb.Append( "\r\ncos:\r\n" );
    for ( k=0; k <= N/2; k++ )
    { for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,6:F1}", cos[k,x]) );
      sb.Append( "\r\n" );
    }
    sb.Append( "sin:\r\n" );
    for ( k=0; k <= N/2; k++ )
    { for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,6:F1}", sin[k,x]) );
      sb.Append( "\r\n" );
    }
    sb.Append( "a:\r\n" );
    for ( k=0; k <=N/2; k++ ) sb.Append( String.Format( "{0,9:F2}", a[k] ) + "\r\n" );
    sb.Append( "b:\r\n" );
    for ( k=0; k <=N/2; k++ ) sb.Append( String.Format( "{0,9:F2}", b[k] ) + "\r\n" );
    sb.Append( "f1:\r\n" );
    for ( x=0; x < N; x++ )   sb.Append( String.Format( "{0,6:F1}", f1[x]) );
    sb.Append( "\r\n" );
  }
  protected override void OnPaint( PaintEventArgs e )
  { e.Graphics.DrawString( sb.ToString(), Font, new SolidBrush( Color.Red ), 0, 0 ); }
}

Дискретная Косинус Трансформация DCT

Мы удлиняем массив f(x) на N-1 элементов и заполняем удлинение симметрично зеркальным отображением относительно середины последнего элемента N-1, путем копирования N-2 → N, N-3 → N + 1, N-4 → N + 2 и т.д. до 0 → N + N-2. Таким образом, мы получим массив нечетной длины 2 * N-1.
Этот массив содержит теперь четную функцию, у которой ось зеркала находится на позиции N-1 + ½. Все значения на одинаковом расстоянии слева и справа от N-1 + ½ являются идентичными:
Для всех 0<=i<=N-2 мы получаем f(N-1-i) == f(N-1+i).
Теперь вы должны позаботиться о том, что косинус-резонаторы имеют экстремум в положении N-1 + ½ и что синус-резонаторы имеют 0 в положении N-1 + ½. В этом случае b_k всегда равны 0. Интегралы умножения f(x) со всеми синус-резонаторами исчезают из-за того, что синус нечетная функция с симметрией в положении N-1 + ½ в то время как косинус является четной функцией с линией симметрии в положение N-1 + ½ так как является зеркальной f(x).
Другими словами, мы просто должны вычислить a_k . Расходы памяти и вычислений остаются прежними, потому что выпадающая часть синус-резонаторов компенсируется удвоением косинус-резонаторов.

Хитрость заключается в том, чтобы ограничить количество косинус-резонаторов очень небольшим числом и игнорировать ошибки, которые за этим последуют. Стало очевидным, что метод DCT является удивительно терпимым к таким сокращениям. Это является причиной, почему он стал современной основой многих эффективных алгоритмов сжатия.

Первым практическим упрощением является намеренно забыть о зеркальном отражении f(x). Существует возможность вычислить все, используя исходный массив длины N, растягивая (на 2 вправо) и сдвигая (на 0,5 влево) косинус-резонаторы.

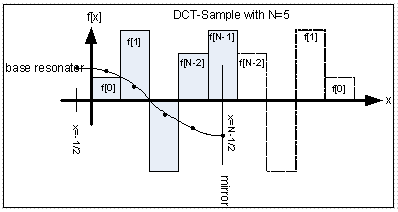
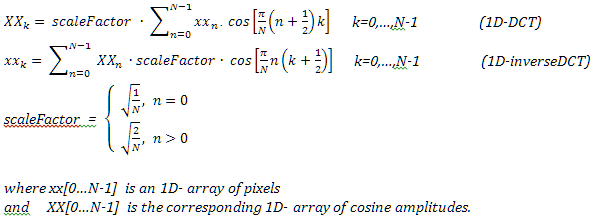
Длина кода алгоритма DCT намного короче, чем соответствующий DFT код ( но время исполнения остается таким же):

using System;
using System.Drawing;
using System.Windows.Forms;
using System.Text;

public class Form1 : Form
{ [STAThread] static void Main() { Application.Run( new Form1() ); }
  const int N = 5;
  float[] f0 = { 1f, 3f, -3f, 2f, 3f }, f1  = new float[N];
  float[,] cos = new float[N,N];
  float[]  a   = new float[N];
  StringBuilder sb = new StringBuilder();
  public Form1()
  { Text = "DCT sample with N=5";
    Width = 320; Height = 400;
    int x, k;
    for ( k=0; k < N; k++ ) //prepare resonators slowly
      for ( x=0; x < N; x++ ) cos[k,x] = Convert.ToSingle( Math.Cos( (x+0.5)*(k+0.5)*Math.PI/N ) );
    for ( k=0; k < N; k++ ) //Discrete Cosine Transform
    { for ( x=0; x < N; x++ ) a[k] += f0[x] * cos[k,x]; //convolution
      a[k] *= 2f/N; //normalization
    }
    for ( k=0; k < N; k++ ) //back transform
      for ( x=0; x < N; x++ ) f1[x] += a[k]*cos[k,x];
    //compose output string
    sb.Append ("f0:\r\n");
    for ( x=0; x < N; x++ )   sb.Append( String.Format( "{0,5:F0}", f0[x]) );
    sb.Append( "\r\ncos:\r\n" );
    for ( k=0; k < N; k++ )
    { for ( x=0; x < N; x++ ) sb.Append( String.Format( "{0,5:F0}", cos[k,x]) );
      sb.Append( "\r\n" );
    }
    sb.Append( "a:\r\n" );
    for ( k=0; k < N; k++ )   sb.Append( String.Format( "{0,9:F2}", a[k] ) + "\r\n" );
    sb.Append( "f1:\r\n" );
    for ( x=0; x < N; x++ )   sb.Append( String.Format( "{0,5:F0}", f1[x]) );
    sb.Append( "\r\n" );
  }
  protected override void OnPaint( PaintEventArgs e )
  {  e.Graphics.DrawString( sb.ToString(), Font, new SolidBrush( Color.Red ), 0, 0 ); }
}

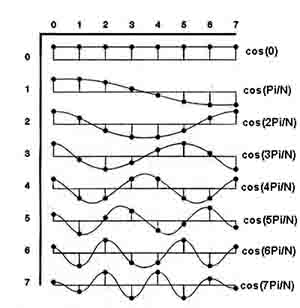
Пример DCT от Виктора Ло с N=8

Следующие таблицы были взяты (и слегка изменены) от Виктора Ло (Victor Lo, City University of Hong Kong: "MPEG 2 Beginners Guide")

Integration of `a₀` and `a₁`	8 cosine-resonators scanned 8 times in `T`

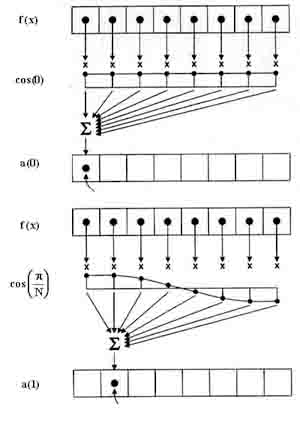Result\Sample Index	0	1	2	3	4	5	6	7
0	+0.707	+0.707	+0.707	+0.707	+0.707	+0.707	+0.707	+0.707
1	+0.981	+0.831	+0.556	+0.195	-0.195	-0.556	-0.831	-0.981
2	+0.924	-0.383	-0.383	-0.924	-0.924	-0.383	+0.383	+0.924
3	+0.831	-0.195	-0.981	-0.556	+0.556	+0.981	+0.195	-0.831
4	+0.707	-0.707	-0.707	+0.707	+0.707	-0.707	-0.707	+0.707
5	+0.556	-0.981	+0.195	+0.831	-0.831	-0.195	+0.981	-0.556
6	+0.383	-0.924	+0.924	-0.383	-0.383	+0.924	-0.924	+0.383
7	+0.195	-0.556	+0.831	-0.981	+0.981	-0.831	+0.556	-0.195